Muhtemelen iş yerinizde şimdiye kadar mümkün olduğunca veriye dayalı kararlar vermişsinizdir. Ancak, size sunulan tüm verileri nasıl ayrıştıracağınızı ya da meslektaşlarınız tarafından oluşturulan analizi doğru bir şekilde nasıl yorumlayacağınızı biliyor musunuz?
Bilmiyorsanız, bugün veri analizinin en önemli türlerinden biri olan regresyonu ve regresyon analizinin nasıl yaıldığını size tüm detayları ile anlatacağız.
Regresyon Nedir?
Regresyon, genellikle finans ve yatırımda kullanılan, bir bağımlı değişken ile bir dizi bağımsız değişken arasındaki ilişkinin gücünü ve niteliğini belirlemeye çalışan istatistiksel bir terimdir.
Regresyon Analizi Nedir?
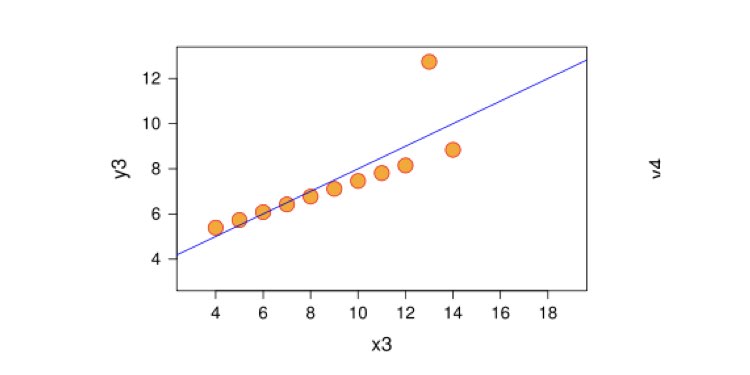
Regresyon analizi, bağımlı değişken ile bağımsız değişken arasındaki ilişkiyi tahmin etmek için kullanılan istatistiksel bir araçtır. Daha spesifik olarak, bağımlı değişkenin bağımsız değişkenlerdeki değişikliklere göre nasıl değiştiğine odaklanır. Ayrıca değişkenler arasındaki gelecekteki ilişkinin modellenmesine de yardımcı olur.
İki değişken varsa, tahminin temelini oluşturan değişken bağımsız değişkendir. Değeri tahmin edilecek değişken bağımlı değişken olarak bilinir.
Örneğin, A, B ve C bağımlı değişkenlerinin bağımsız değişken D’yi nasıl etkilediğini öğrenmek istiyorsunuz diyelim. “A artarsa, D üzerinde B veya C’den daha fazla etkisi olur mu?”, “C azalırsa, D üzerinde A veya B’den daha fazla etkisi olur mu?” vb. soruların cevaplarını bulmanıza yardımcı olur.
Regresyon analizi, doğrusal, doğrusal olmayan ve çoklu doğrusal olmak üzere çeşitli türlerden oluşur. Ancak en kullanışlı regresyon türleri, basit doğrusal ve çoklu doğrusal regresyondur.
Bulutistan hizmetlerinin detaylarına ulaşmak için tıklayınız.
Regresyon Denklemi ve Tahmin
Regresyon analizi formülü:
Formül Y = MX + b
- Y, regresyon denkleminin bağımlı değişkenidir.
- M, regresyon denkleminin eğimidir.
- X, regresyon denkleminin bağımlı değişkenidir.
- b denklemin sabitidir.
Regresyon Ne İşe Yarar?
Regresyonun ne işe yaradığını basit bir örnekle aşağıda sizin için açıkladık.
Örneğin, kahveyi ne tür insanların satın aldığına ilişkin verileri tahmin etmek istediğinizi varsayalım. Yani, bu durumda, kahve satın alan ve yaşı, boyu, mali durumu vb. bilgiler gibi kişi verilerini bulacaksınız.
Bu verileri analiz ettikten sonra, bir kişinin kahveyi alıp almayacağını tahmin etmek için bir model oluşturmanız gerekir. Dolayısıyla, bağımlı değişkenin davranışını büyük bağımsız değişkenlere dayanarak tahmin etmek için regresyon analizinin kullanıldığını söyleyebiliriz.
Regresyon Analizi Nasıl Yapılır?
Bir regresyon analizi 3 adımda gerçekleştirilir:
1. Bir hipotez oluşturun
Bir regresyon analizi yapmak için, ilişkili olduğuna inandığınız iki değişkeni seçmeniz gerekir. Mümkün olduğu kadar çok veri toplayarak ilişkileri hakkında hipotezinizi oluşturun. Reklam ve satış ilişkisi söz konusu olduğunda, daha doğru bir analiz için bir yıl boyunca oluşan tüm finansal verileri toplayabilirsiniz.
2. Bir grafik oluşturun
Bir sonraki adım, verilerinizin grafiğini çıkarmaktır. İki veri seti ile doğrusal regresyon için temel bir çizgi grafiği oluşturabilirsiniz. Bir değişken X ekseninde, diğeri Y ekseninde çizilir. Bir elektronik tabloya girdiğinizde, değişkenler arasındaki korelasyonu görebilirsiniz. Düz bir çizgi varsa, bu pozitif bir korelasyon gösterir.
3. Sonuçları analiz edin
Grafiği temel bir doğrusal regresyonda inceleyerek kesişim, katsayı ve korelasyonu görebilirsiniz. Bu rakamları bir araya getirmek, iki veri seti arasındaki tarihsel ilişkiyi göstererek modelin gelecekte nasıl görüneceğini tahmin etmenize olanak tanır. Geçmişte, çevrimiçi reklamcılık ve satışlar arasında olumlu bir ilişki varsa, gelecek yıl için bir tahmin oluşturmak için yüzdeleri bir modele ekleyebilirsiniz.
Regresyon Analizi Kullanım Alanları
Aşağıdaki listede regresyon analizinin kullanım alanlarını bulabilirsiniz:
1. Tahmin
İşletmelerde regresyon analizinin en yaygın kullanımı, gelecekteki fırsatları ve tehditleri tahmin etmektir. Örneğin talep analizi, bir müşterinin satın alma olasılığı yüksek olan şeylerin miktarını tahmin eder.
Ancak iş söz konusu olduğunda, talep tek bağımlı değişken değildir. Regresif analiz, doğrudan gelirden çok daha fazlasını öngörebilir.
Örneğin, belirli bir reklam panosunun önünden geçecek tüketicilerin sayısını tahmin ederek bir reklam için en yüksek teklifi tahmin edebilir.
2. CAPM
Bir varlığın öngörülen getirisi ile ilgili piyasa risk primi arasındaki bağlantıyı kuran The Capital Asset Pricing Model (CAPM), doğrusal regresyon modeline dayanır. Ayrıca, kurumsal getirileri ve operasyonel performansı tahmin etmek için finansal analistler tarafından finansal analizde sıklıkla kullanılır.
Bir hisse senedinin beta katsayısı, regresyon analizi kullanılarak hesaplanır. Beta, toplam piyasa riskiyle ilgili getiri oynaklığının bir ölçüsüdür.
3. Rekabet karşılaştırma
Bir şirketin finansal performansını belirli bir muadili ile karşılaştırmak için kullanılabilir. Ayrıca iki firmanın hisse senedi fiyatları arasındaki ilişkiyi belirlemek için de kullanılabilir ve hangi yönlerin satışlarını etkilediğini belirlemede firmaya yardımcı olabilir. Bu teknikler, küçük işletmelerin kısa sürede hızlı başarıya ulaşmalarına yardımcı olabilir.
4. Güvenilir kaynak
Birçok işletme ve üst düzey yönetici, daha iyi iş kararları vermek, varsayımları ve içgüdüleri azaltmak için regresyon analizini kullanır. Yöneticiler, verileri filtrelemek ve mümkün olan en iyi kararları vermek için regresyon analizinden yararlanır.
Regresyon Analizinde Kullanılan Terminolojiler Nelerdir?
1. Outliers (Aykırı Değerler)
Aykırı değerler, bir veri kümesindeki normal dağılıma uymayan ve herhangi bir regresyon modelini önemli ölçüde bozma potansiyeline sahip anormal değerler olarak tanımlanır. Bu nedenle, verilerden doğru içgörü elde etmek için aykırı değerler dikkatli bir şekilde ele alınmalıdır. Genellikle, gerçek dünyadan toplanan veriler, çeşitli özelliklerde çeşitli gözlemlerden oluşur ve değerlerin çoğu yanlış yerleştirilmiş olabilir. Aykırı değerlerin nedeni ne olursa olsun, aykırı değerler analiz edilmeli ve bunların gerçek olup olmadığı doğrulanmalıdır. Aykırı değerler gerçekse, bu aykırı değerler bir regresyon modeline alınabilir veya daha iyi bir regresyon modeli yapmak için basitçe bırakılabilir.
2. Multicollinearity (Çoklu Doğrusallık)
Çoklu doğrusallık, bir regresyon modelinde iki veya daha fazla bağımsız değişken birbiriyle yüksek düzeyde ilişkili olduğunda ortaya çıkar.
Bu, bir regresyon modelinde bağımsız bir değişkenin başka bir bağımsız değişkenden tahmin edilebileceği anlamına gelir. Örneğin, boy ve kilo, hane geliri ve su tüketimi, bir arabanın kilometresi ve fiyatı, çalışma zamanı ve boş zaman vb.
3. Heteroskedastisite
Heteroskedastisite, artıkların varyansının bir dizi ölçülen değer üzerinde eşit olmadığı durumları ifade eder. Bir regresyon analizi çalıştırırken, değişen varyans, artıkların eşit olmayan bir şekilde dağılmasıyla sonuçlanır (hata terimi olarak da bilinir).
Artıkların grafiğini gözlemlerken, bir yelpaze veya koni şekli, değişen varyanslılığın varlığını gösterir. İstatistikte, değişen varyanslılık bir problem olarak görülür, çünkü sıradan en küçük kareleri (OLS) içeren regresyonlar, artıkların sabit varyanslı bir popülasyondan alındığını varsayar.
Eşit olmayan bir artık dağılımı varsa, regresyonda kullanılan popülasyon eşit olmayan varyans içerir ve bu nedenle analiz sonuçları geçersiz olabilir.
4. Underfit ve Overfit (Yetersiz Uyum ve Aşırı Uyum)
Gereksiz açıklayıcı değişkenler kullandığımızda, aşırı uyuma neden olabilir. Aşırı uyum, algoritmamızın eğitim setinde iyi çalıştığı, ancak test setlerinde daha iyi performans gösteremediği anlamına gelir. Aynı zamanda yüksek varyans problemi olarak da bilinir.
Algoritmamız o kadar kötü çalışıyor ki bir eğitim setine bile tam olarak uyamıyorsa, o zaman verinin yetersiz olduğu söylenir. Yetersiz uyum sorunu olarak da bilinir.
Regresyon Türleri Nelerdir?
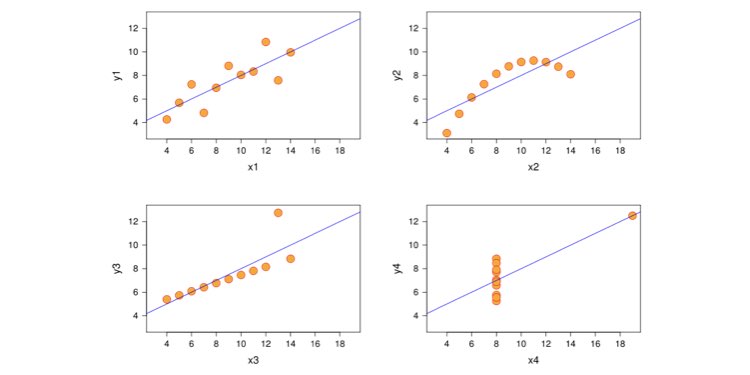
Aşağıda en yaygın regresyon türü ve özelliklerini bulabilirsiniz:
1. Doğrusal Regresyon
Doğrusal bir regresyon, tamamen doğrusal değişkenlerden oluşan bir regresyon modelini ifade eder. Karmaşık sistemlerin davranışını anlamanıza ve tahmin etmenize veya deneysel, finansal ve biyolojik verileri analiz etmenize yardımcı olabilir.
Doğrusal bir regresyon modeli için genel denklem aşağıdaki şekildedir:
Y=β0+∑ βiXi+ϵi
Burada β hesaplanacak doğrusal parametre tahminlerini, ϵ ise hata terimlerini temsil eder.
İki tür doğrusal regresyon analizi vardır: Basit regresyon (simple regression) ve çoklu regresyon (multiple regression).
Basit regresyon, tek bir açıklayıcı değişken kullanırken çoklu regresyon çok sayıda açıklayıcı değişken kullanır.
Basit doğrusal regresyon, büyük boyutlu veriler için uygun değildir. Burada yalnızca bir bağımlı ve bir bağımsız değişken vardır, bağımsız ve bağımlı değişkenler arasındaki ilişki doğrusaldır ve regresyon çizgisinin türü düz bir çizgidir.
Çoklu doğrusal regresyon ise, bir bağımlı değişken ve birden çok bağımsız değişken içerir.
Sonuçlar elde edildikten sonra bağımsız değişken bilinen bir faktör olduğunda, bağımlı değişkenin tahmin edilmesine yardımcı olur. Bu, regresyon istatistiklerinin yardımıyla yapılır.
Basit regresyon denklemi:
Y = a+bX+u
Y = Bağımlı değişken
X = Bağımsız (Açıklayıcı) değişken
a = Kesişme, b= Eğim, u= Regresyon kalıntısı
Çoklu regresyon denklemi:
Y = a+bX1+cX2+dX3+eX4+…….+tXt+u
Y = Bağımlı değişken,
X1, X2, X3, X4 = Bağımsız (Açıklayıcı) değişkenler,
a = Kesişme,
b,c,d = Eğimler,
u = regresyon kalıntısı
Regresyon kalıntısı, tahmin değeri ile gözlemlenen değer arasındaki farktır.
2. Kademeli Doğrusal Regresyon (Stepwise Linear Regression)
Bu tür regresyon analizi, birden fazla bağımsız değişkenle çalıştığınızda yardımcı olur. Adım adım regresyonda üç yöntem kullanılır.
3. Polinomsal Regresyon (Polynomial Regression)
Bağımlı değişken “x” ve bağımsız değişken “y” değerlerinin ilişkisini doğrusal olmayan olarak modelleyen bir regresyon analizi türüdür. Verilere doğrusal olmayan bir model sığdırsa da, çoklu doğrusal regresyonun özel bir durumudur.
4. Lojistik Regresyon (Logistic Regression)
Lojistik regresyon, biyoloji alanında ilk kez 20. yüzyılda kullanılan bir yöntemdir. Mutlu/üzgün, normal/anormal veya başarılı/başarısız gibi birbirini dışlayan belirli olayların olasılığını tahmin etmek için kullanılır. Olasılığın değeri kesinlikle 0 ile 1 arasında değişir.
5. Ridge Regresyon
Bu tip regresyon, çoklu regresyondan elde edilen verilerin incelenmesi için kullanılır.
6. Lasso Regresyon
Bu tip regresyon, ridge regresyon ile aynıdır, ancak tek fark, sürekli bilginin tipik olmamasıdır.
7. Kantil Regresyon (Quantile Regression)
Kuantil regresyon, lineer regresyonu kullanmak için gerekli koşullar tam olarak sağlanmadığında kullanılan ekonometrik bir tekniktir. Bu, lineer regresyon analizinin bir uzantısıdır, yani, lineer regresyona kıyasla aykırı değerlere karşı tahminleri güçlü olduğundan, verilerde aykırı değerler mevcut olduğunda kullanılabilir.
8. Elastik Net Regresyon
Elastik net regresyon, aşırı derecede ilişkili bağımsız değişkenlerle uğraşmak zorunda kaldığında, ridge ve lasso regresyona tercih edilir.
9. Sıralı Regresyon (Ordinal Regression)
Sıralı regresyon, sıralanmış değerleri önceden göstermek için kullanılır. Teknik, bağımlı değişken sıralı olduğunda kullanışlıdır.
Doğrusal Regresyon Nedir?
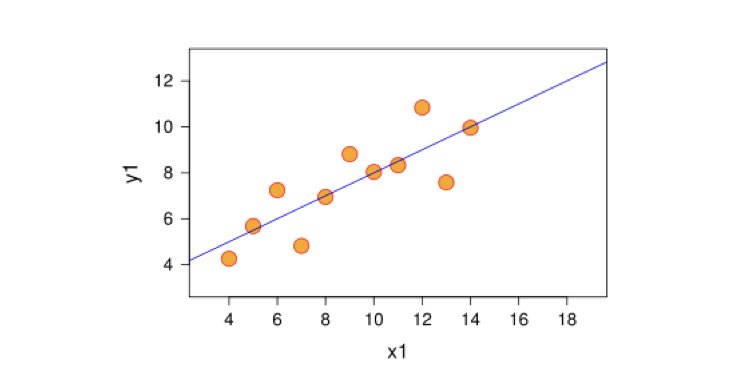
Doğrusal regresyon, iki değişken arasındaki ilişkiyi göstermeye çalışan bir tür istatistiksel analizdir. Çeşitli veri noktalarına bakar ve bir eğilim çizgisi çizer. Doğrusal regresyon, kanser teşhisi veya hisse senedi fiyatları gibi verilerdeki eğilimleri gösteren, görünüşte rastgele veriler üzerinde tahmine dayalı bir model oluşturabilir.
Doğrusal regresyon, analitikte önemli bir araçtır. Teknik, bir dizi veri noktasında bir eğilim çizgisi çizmek için istatistiksel hesaplamaları kullanır. Trend çizgisi, cilt kanseri teşhisi konan kişi sayısından bir şirketin finansal performansına kadar her şey olabilir. Doğrusal regresyon, bağımsız bir değişken ile incelenen bağımlı bir değişken arasındaki ilişkiyi gösterir.
Doğrusal regresyonu hesaplamanın birkaç yolu vardır. En yaygın olanlardan biri, verilerdeki bilinmeyen değişkenleri tahmin eden ve görsel olarak veri noktaları ile eğilim çizgisi arasındaki dikey mesafelerin toplamına dönüşen sıradan en küçük kareler yöntemidir.
Doğrusal regresyonları gerçekleştirmek için yapılan hesaplamalar oldukça karmaşık olabilir. Neyse ki, doğrusal regresyon modelleri Excel, R, MATLAB ve Mathematica gibi çoğu büyük hesaplama paketine dahil edilmiştir.
Regresyon Analizi için Doğru Regresyon Modeli Nasıl Seçilir?
Regresyon analizi, bir dizi bağımsız değişken ile bir bağımlı değişken arasındaki ilişkiyi matematiksel olarak tanımlar. Kullanabileceğiniz çok sayıda regresyon modeli vardır. Bu seçim genellikle bağımlı değişken için sahip olduğunuz verinin türüne ve en iyi uyumu sağlayan modelin türüne bağlıdır.
Regresyon Analizi Örnekleri
Regresyon analizinin nerelerde kullanılabileceğini öğrenmek istiyorsanız, aşağıdaki örnekleri inceleyebilirsiniz.
Finansta, bir hisse senedinin BETA’sını hesaplamak için regresyon analizi kullanılır. Üstelik bunu Excel yardımı ile kolayca yapabilirsiniz.
Yine finansta, şirketler için mali tabloları tahmin etmek için regresyon analizi de kullanılır. Böylece, iş varsayımlarındaki hangi değişikliklerin gelecekteki giderleri ve geliri etkileyeceğini belirleyebilirsiniz.
Bir şirketin satışları son birkaç yıldır her ay istikrarlı bir şekilde arttıysa, satış verileri üzerinde aylık satışlarla doğrusal bir analiz yaparak şirketin gelecek aylardaki satışlarını tahmin edebilirsiniz.
Bir firmanın yöneticisi, gelecek planlaması için reklam harcamaları ile satışlar arasındaki kesin ilişkiyi öğrenmek istiyorsa, regresyon tekniği ile bu ilişkiyi tahmin edebilir.
Bulutistan hizmetlerinin detaylarına ulaşmak için tıklayınız.
İşletmeler Neden Regresyon Analizi Yapmalıdır?
İşinize rehberlik etmenize yardımcı olacak bazı regresyon uygulamaları aşağıdaki şekildedir:
1. Diğer Kalıpları Anlamak
Regresyon analizinin yardımıyla verilerde ortaya çıkan her türlü kalıbı anlayabilirsiniz. Ayrıca, bu yeni anlayışların işinizde nasıl bir fark yaratacağını anlamanız için bu bilgiler sizin için çok değerli olacaktır.
2. Hataları Düzeltme
Regresyon analizi yalnızca daha iyi bir karar oluşturmaya yardımcı olmakla kalmaz. Ayrıca yargılardaki hataları bulmanıza da yardımcı olur. Çeşitli faktörlere bakarak karar vermeniz için size nicel destek sağlar ve hataların önüne geçer.
3. Optimizasyon Süreci
Daha fazla veriyi anlayarak verimliliğinizi artırabilir ve işletmenize tam fayda sağlamak için süreçleri iyileştirebilirsiniz. Ayrıca verilerle optimize edilen süreçler işletmelerin daha akıllı çalışmasına da yardımcı olacaktır.
Korelasyon vs. Regresyon Arasındaki Farklar
Korelasyon ve regresyon birbiriyle çok sık karıştırılır, çünkü korelasyon genellikle regresyona neden olabilir. Ancak, aralarında önemli bir fark vardır.
Bu iki istatistiksel ölçüm arasındaki fark, korelasyonun iki değişken (x ve y) arasındaki ilişkinin derecesini ölçmesi, regresyonun ise bir değişkenin diğerini nasıl etkilediğidir.
- Regresyon, x’in y’nin değişmesine nasıl neden olduğunu ve x ile y değiştirilirse sonuçların nasıl değişeceğini belirler. Korelasyon ile x ve y, değiş tokuş edilebilen ve aynı sonucu alabilen değişkenlerdir.
- Korelasyon, tek bir istatistik veya veri noktası iken, regresyon, bir çizgi ile temsil edilen tüm veri noktalarıyla denklemin tamamıdır.
- Korelasyon iki değişken arasındaki ilişkiyi gösterirken, regresyon birinin diğerini nasıl etkilediğini görmemizi sağlar.
- Regresyonla gösterilen veriler, biri değiştiğinde diğeri de her zaman aynı yönde değişmez, bir neden ve sonuç oluşturur. Korelasyon ile değişkenler birlikte hareket eder.
















