Günlük hayatta birbiriyle ilişkili birçok nicelik vardır. Örneğin, meyvelerin fiyatı ağırlıklarıyla ilişkilidir, birinin kilosu boyuyla ilişkili olabilir veya Fahrenheit Santigrat derece cinsinden karşılığı vardır.
Birbiriyle ilişkili olabilecek iki sayı kümeniz varsa, bunları ilişkilendiren denklemi bulmanız gerekir.
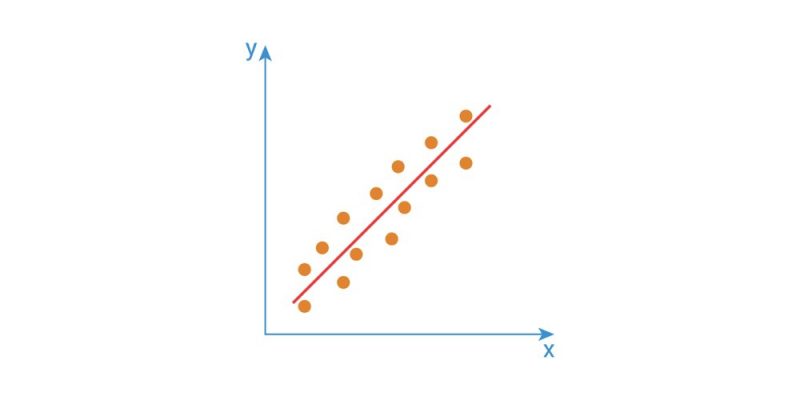
İlişkinin doğrusal olduğunu düşünüyorsanız, bu noktada doğrusal regresyon kullanabilirsiniz.
Peki doğrusal regresyon nedir?
Doğrusal (Linear) Regresyon Nedir?
Doğrusal (linear) regresyon, bağımsız bir değişken ile bağımlı bir değişken arasındaki ilişki hakkında daha fazla bilgi edinmek için kullanılan istatistiksel bir tekniktir. Analizinizde birden fazla bağımsız değişken olduğunda, bu çoklu doğrusal regresyon olarak adlandırılır.
Bunu aşağıdaki denklem ile ifade edebiliriz:
Yi=β0+β1Xi+ϵi
Bu denklem, tek bir açıklayıcı değişken olması durumunda basit doğrusal regresyon, birden fazla açıklayıcı değişken olması durumunda ise, çoklu doğrusal regresyon olarak adlandırılır.
Regresyon analizinde, örneklem için bağımlı ve bağımsız değişkenler arasındaki ilişkileri bularak popülasyonun geneli hakkında çıkarımlarda bulunmak amaçlanır. Regresyon katsayılarını tahmin etmek için genellikle OLS (Ordinary Least Squares) yöntemi kullanılır. OLS, hataların karelerinin toplamını minimize ederek en iyi katsayıları bulur.
Bulutistan hizmetlerinin detaylarına ulaşmak için tıklayınız.
Doğrusal Regresyon için Varsayımlar
Doğrusal regresyonu uygulamak için öncelikle aşağıdaki koşulları kontrol etmeniz gerekir:
1. Nicel değişken koşulu
Korelasyon yalnızca her iki değişkenin de nicel olması durumunda geçerlidir.
2. Yeterince düz olma koşulu
Dağılım grafiğine bakın ve verilerinizin yaklaşık olarak doğrusal bir ilişkiye sahip olduğundan emin olun. Korelasyon yalnızca doğrusal bir ilişkinin gücünü ölçer.
3. Aykırı değer durumu
Aykırı değerler korelasyonu bozabilir. Aykırı değerler mevcut olduğunda, en iyi yol, aykırı değerleri içeren bir korelasyon ve aykırı değerleri içermeyen başka bir korelasyon hesaplamaktır.
Doğrusal Regresyon Hakkında Notlar
Doğrusal regresyonun ilk adımı doğrusallık varsayımını test etmektir. Bu, bağımlı ve bağımsız değişkenler arasındaki ilişkiyi gözlemlemek için değerleri dağılım grafiği olarak bilinen bir grafikte çizerek gerçekleştirilebilir. Veriler üstel olarak dağılmışsa, regresyon denklemini oluşturmanın bir anlamı yoktur.
Doğrunun matematiksel denklemi y=a+bx+ε şeklindedir.
- b – Doğrunun eğimi
- a – x=0 olduğunda y-kesişimi
- Rastgele hata (ε-Epsilon) – Belirli bir x değeri için y’nin gözlenen değeri ile y’nin ortalama değeri arasındaki fark.
Basit Bir Doğrusal Regresyon Modeli İçin Formül
Basit doğrusal regresyon analizinde yer alan iki faktör x ve y olarak adlandırılır. Y’nin x ile nasıl ilişkili olduğunu açıklayan denklem regresyon modeli olarak bilinir.
Basit doğrusal regresyon modeli aşağıdaki şekilde gösterilir:
y = β0 +β1x+ε
Doğrusal regresyon modeli, ε ile temsil edilen bir hata terimi içerir. Hata terimi, x ve y arasındaki doğrusal ilişki ile açıklanamayan y değişkenliğini açıklamak için kullanılır. ε olmasaydı, bu, x’in bilinmesinin y değerini belirlemek için yeterli bilgi sağlayacağı anlamına gelirdi.
Ayrıca incelenen popülasyonu temsil eden parametreler de vardır. Modelin bu parametreleri β0 ve β1 ile temsil edilir.
Basit doğrusal regresyon denklemi düz bir çizgi olarak grafiklendirilir, bu grafikte;
- β0 regresyon doğrusunun y-kesişimidir.
- β1 eğimdir.
- Ε(y), belirli bir x değeri için y’nin ortalama veya beklenen değeridir.
Bir regresyon çizgisi pozitif doğrusal bir ilişki, negatif doğrusal bir ilişki gösterebilir veya hiçbir ilişki göstermeyebilir.
İlişki yok: Basit doğrusal regresyonda grafiği çizilen çizgi düzdür (eğimli değildir). İki değişken arasında hiçbir ilişki yoktur.
Pozitif ilişki: Regresyon çizgisi, çizginin alt ucu grafiğin y-kesişiminde (ekseninde) olacak şekilde yukarı doğru eğimlidir ve çizginin üst ucu grafik alanına doğru, x-kesişiminden (ekseninden) uzağa doğru uzanır. İki değişken arasında pozitif doğrusal bir ilişki vardır. Birinin değeri arttıkça diğerinin değeri de artar.
Negatif ilişki: Regresyon çizgisi, çizginin üst ucu grafiğin y-kesişiminde (ekseninde) olacak şekilde aşağıya doğru eğimlidir ve çizginin alt ucu grafik alanında aşağıya, x-kesişimine (eksenine) doğru uzanır. İki değişken arasında negatif doğrusal bir ilişki vardır. Birinin değeri arttıkça diğerinin değeri azalır.
Tahmin Edilen Doğrusal Regresyon Denklemi
Popülasyonun parametreleri biliniyorsa, bilinen bir x değeri için y’nin ortalama değerini hesaplamak için basit doğrusal regresyon denklemi kullanılabilir:
Ε(y) = β0 +β1x+ε
Ancak uygulamada, parametre değerleri genellikle bilinmemektedir, bu nedenle popülasyonun bir örneğinden elde edilen veriler kullanılarak tahmin edilmeleri gerekir. Popülasyon parametreleri örneklem istatistikleri kullanılarak tahmin edilir. Örneklem istatistikleri β0 ve β1 ile temsil edilir. Örnek istatistikleri popülasyon parametreleri ile yer değiştirdiğinde, tahmini regresyon denklemi oluşturulur.
Tahmin edilen regresyon denklemi aşağıdaki şekildedir:
(ŷ) = β0 +β1x+ε
Tahmin edilen basit regresyon denkleminin grafiğine tahmin edilen regresyon doğrusu denir.
- β0 regresyon doğrusunun y-kesişimidir.
- β1 ise eğimdir.
- (ŷ), belirli bir x değeri için y’nin tahmini değeridir.
Doğrusal Regresyon Ne Zaman Kullanılır?
Basit doğrusal regresyonda, tek bir bağımlı değişkeni tahmin etmek için kullanılan tek bir bağımsız değişken vardır. Çoklu doğrusal regresyonda ise tek bir bağımlı değişkeni tahmin etmek için birden fazla bağımsız değişken kullanılır. Aslında, basit ve çoklu regresyon arasındaki temel fark açıklayıcı değişkenlerin varlığından kaynaklanır.
Örneğin, mahsul verim oranını bir mevsimdeki yağış oranıyla karşılaştırırken doğrusal regresyon kullanabilirsiniz.
Doğrusal Regresyon Neden Kullanılır?
Doğrusal regresyon, regresyon analizi yapmak için kullanılır. Aşağıda regresyon analizinin kullanım alanları yer almaktadır.
- Tahmin edicilerin gücünü belirlemeye yardımcı olur: Bu teknik satış ve pazarlamada kullanılır. Öngörücü analiz, öngörücü ve sonuç değişkeni (yani doz ve etki) arasındaki ilişkiyi anlamaya yardımcı olur.
- Tahmin yoluyla etkiyi öngörme: Bağımlı değişkendeki değişim, bağımsız değişkende bir farklılığa neden olacaktır. Örneğin, bir ürünü pazarlamak için daha fazla para harcarsanız, bu durum satışların artmasını veya azalmasını etkileyebilir.
- Trend analizi / tahmin: Regresyon analizi, özellikle fiyatlarda dalgalanmaların ve enflasyonun olduğu hisse senedi piyasasında gelecekteki eğilimleri tahmin etmek için kullanılır.
Doğrusal Regresyon Türleri
Aşağıdaki listede 5 tür doğrusal regresyon türünü bulabilirsiniz:
1. Basit Doğrusal Regresyon
Basit regresyonda bir bağımlı değişken (aralık veya oran), bir bağımsız değişken (aralık veya oran veya ikili) vardır. Örnek olarak bir çocuğun boyunun her büyüme yılında ölçülmesi verilebilir. Bunun gibi birçok gerçek dünya örneği basit doğrusal regresyon altında kategorize edilir.
2. Çoklu Doğrusal Regresyon
Çoklu regresyon, iki bağımsız değişken ve bir bağımlı değişken olduğunda kullanılır. Bağımsız değişkenlerin bağımlı değişken üzerinde nasıl bir etkiye sahip olduğunu bu sayede belirleyebiliriz.
Çoklu regresyonda, x’i bir dizi bağımsız değişken (x1, x2…) ve Y’yi bağımlı değişken olarak varsayabilirsiniz. Ayrıca bir regresyon değişkeninin eğimi olarak b’ye sahip olursunuz. Aşağıda x ve y arasındaki ilişkiyi temsil eden denklemi bulabilirsiniz:
Y = a + b1x1 + b2x2 + …
Çoklu regresyon analizi yapılırken değişkenlerin seçimi de önemlidir. Bir model oluşturmadan önce önemli değişkenlerin ve önemsiz değişkenlerin neler olduğunu anlamanız gerekir.
3. Lojistik Regresyon
Lojistik regresyon, bir bağımlı değişken ve iki bağımsız değişken olduğunda yapılır. Çoklu ve lojistik regresyon arasındaki fark, hedef değişkenin kesikli olmasıdır (ikili veya sıralı bir değer). Doğrusal regresyonla ilgili sorun, değişken değerinin yalnızca iki olası sonuca sabitlenmiş olmasıdır. Öte yandan lojistik regresyon, belirli bir olayın meydana gelmesini yansıtan bir olasılık puanı döndürebilir.
Lojistik regresyon, spam e-posta’ların tespit edilmesi, bir müşterinin kredi tutarının tahmin edilmesi, bir kişinin belirli bir ürünü satın alıp almayacağı gibi birçok farklı durumda kullanılır. Lojistik regresyon, bir olayın meydana gelme olasılığını belirlemede kullanışlıdır. Lojistik regresyon çeşitli makine öğrenimi algoritmalarında kullanılır.
4. Ordinal Regresyon
Ordinal regresyon, bir bağımlı ikili değişken ve sıralı veya nominal olabilen bir bağımsız değişken üzerinde gerçekleştirilir. Ordinal regresyon, Genelleştirilmiş Doğrusal Model (GLM) kullanılarak gerçekleştirilebilir ve makine öğrenimi terimlerinde buna sıralama analizi de denir.
Pazarlamada ordinal regresyon, bir ürünün satın alınmasının bir tüketicinin ilgili bir ürünü satın almasına yol açıp açmayacağını tahmin etmek için kullanılır. Örneğin, bir tüketici pizza satın alırsa, yanında bir meşrubat sipariş etme olasılığı nedir? Bu noktada alkolsüz içeceğin miktarı da göz önünde bulundurulmalıdır. Meşrubat siparişini, sipariş edilen pizzanın boyutu ve siparişle birlikte verilen ikramlar gibi çeşitli faktörler de etkiler.
5. Multinomial Regresyon
Multinomial regresyon, bir nominal bağımlı değişken ve oran, aralık veya ikili olan bir bağımsız değişken üzerinde yapılır.
Multinomial regresyona örnek olarak, ebeveynin mesleğine ve eğitimine bağlı olan öğrenciler arasındaki mesleki tercihler verilebilir.
Regresyon Analizi Neden Önemlidir?
Aşağıdaki listede regresyon analizinin neden önemli olduğuna dair bir liste bulabilirsiniz:
- Regresyon analizi, çeşitli veri noktalarını ve bunlar arasındaki ilişkiyi anlamaya yardımcı olur. Özellikle iş modellerinde önemli olduğu düşünülmektedir.
- Regresyon analizi ayrıca tahmin ve öngörü için de kullanılır.
- Verileri ve aralarındaki ilişkiyi anlamak, işletmelerin büyümesine ve belirli eğilimleri veya kalıpları analiz etmesine yardımcı olur. Bu, işletmelere yeni içgörüler sağlayabilir.
- Veri noktalarını çizerken, regresyon analizi bir şirketin başarısızlıklarını anlamaya ve hatalardan kaçınarak başarılı olmak için bunları düzeltmeye yardımcı olur. Bu tür bir analiz, piyasaya yeni bir ürün sürüldüğünde ve bu ürünün başarısını belirlemede yardımcı olur.
- Regresyon analizi ayrıca şirketin maksimum verimlilik sağlamasına ve süreçlerini iyileştirmesine yardımcı olur.
Doğrusal Regresyonun Sınırlamaları
Doğrusal regresyon en popüler modellerden biridir. Bağımlı ve bağımsız değişkenlerin doğrusal bir ilişkiye sahip olduğunu bildiğimizde, basitliği ve yorumlama kolaylığı nedeniyle bu en iyi seçenektir. Bununla birlikte, aşağıda belirtilen bazı sınırlamaları vardır:
1. Bazı durumlarda basittir
Doğrusal regresyon modeli, temel koşullar sağlandığında bağımlı ve bağımsız değişkenler arasında doğrusal bir ilişki olan veriler için mükemmeldir. Ancak durum her zaman böyle değildir. Birçok gerçek dünya uygulaması için özellikle de zaman serisi verileriyle uğraşırken…
Doğrusal olmayan ilişkiler için (artık grafiğinizde bir eğri gördüğünüzde), lojistik regresyon kullanmak daha iyi bir seçenek olacaktır.
Zaman serisi verileri için doğrusal regresyon modelinin temel varsayımı, altta yatan serinin durağan olmasıdır. Ancak bu, orijinal haliyle durağan olmayan çoğu ekonomik seri için geçerli değildir.
2. Aykırı değerlere duyarlılık
Doğrusal regresyon modeli, katsayıları tahmin etmek için OLS modelini kullanır. Bu model, hataların karesel toplamını en aza indirerek en uygun doğruyu bulur. Dolayısıyla, ana nokta kümesinden uzakta olan herhangi bir gözlem karesel bir etkiye sahip olacaktır. Sonuç olarak, aykırı değerler modelin çıktısı üzerinde büyük bir etkiye sahip olabilir.
3. Yetersiz uyum eğilimli
Yetersiz uyum, bir model verilerin altında yatan yapıyı yeterince yakalayamadığında ortaya çıkar. Doğrusal regresyon modelinin tanımında yer alan çeşitli varsayımlar nedeniyle, gerçek hayattaki uygulamaların çoğunun karmaşıklığını yakalayamaz. Bu tür durumlarda bu modelin doğruluğu düşüktür.
4. Karmaşık modellere aşırı uyum
Yetersiz uyumun aksine aşırı uyum, model verilere çok iyi uyduğunda gerçekleşir. Bu yüzden test verilerinde iyi performans göstermez. Doğrusal regresyonda bu genellikle model çok sayıda parametreyle çok karmaşık olduğunda ve veriler çok az olduğunda meydana gelir.
Sonuç olarak, doğrusal regresyon finans, ekonomi, tıp, spor vb. gibi birçok alanda kullanılan basit ama güçlü bir modeldir. Bu modelin arkasındaki varsayımları ve nerede yetersiz kaldığını anlamak, onu daha iyi kullanmamızı sağlar.
Bulutistan hizmetlerinin detaylarına ulaşmak için tıklayınız.
Doğrusal Regresyon Hakkında Sıkça Sorulan Sorular
1. Doğrusal regresyon nedir?
Doğrusal regresyon, bağımlı bir değişken ile bir veya daha fazla bağımsız değişken arasındaki ilişkiyi tanımlayan en iyi düz çizgiyi bulmaktan oluşan istatistiksel bir tekniktir.
2. Regresyon doğrusu nedir?
Regresyon doğrusu, iki değişken arasındaki doğrusal davranışı en iyi tanımlayan ve ondan tahminler yapmanızı sağlayan doğrudur.
3. Doğrusal regresyon bir sınıflandırma algoritması mıdır?
Hayır, doğrusal regresyon bir regresyon algoritmasıdır.
4. Doğrusal regresyon ne zaman kullanılır?
Verilerinizin dağılım grafiği doğrusal bir davranışa sahip olduğunda, doğrusal regresyonu kullanabilirsiniz.